- 17
- Sep
- 2015
Sud, izjava i istinitost
U matematici se pod sudom ili izrekom podrazumeva izreka – ali ne bilo kakva. Da bi se izreka nazvala sudom ona mora biti suvisla, smislena izreka i mora biti ili tačna ili netačna. Siva zona ne sme da postoji. Da li je svaka izreka sud? Naravno da nije. Evo i nekoliko primera izreka koji nisu sudovi:
1. Klovn pleše po oblacima sa svilenim duhom. – Ova izreka je bez smisla, nesuvisla je.
2. Parni valjak skače po bini. – Ova izreka je bez smisla, nesuvisla je.
Kod primera 2. moramo biti veoma oprezni. Za nekog ova izreka je suvisla, a za nekog nesuvisla. Ukoliko se neko trenutno nalazi na koncertu grupe “Parni valjak” ova izreka svakako može da ima smisla i da bude istinita ili neistinita. Za one druge koji nisu deo tog referentnog okvira takva izreka je u potpunosti nesuvisla.
Pored nesuvislih ima i izreka koje nisu ni istinite ni neistinite. Primer je izreka: “Trči na trening!”. U potpunosti je smislena, ali se ne može govoriti o njenoj istinitosti ili neistinitosti.
Bilo bi zaista lepo kada bi takva situacija bila i u sudovina (privrednim, vrhovnim, apelacionim i sl.) i kada bi jasno moglo da se utvrdi da li je nešto smisleno ili ne, istinito ili ne i to u referentnom okviru važećih zakona.
Da ne bi svaki put pisali čitavu izreku koja predstavlja sud, matematičari te izreke obično označavaju velikim slovima abedede: A, B, C, D… Tim sudovima se dodeljuje vrednost tačno ili netačno koja se čina “te” (T) ili “ne-te”
U praksi to izgleda ovako:
A vi sada pokušajte da zamislite sudsku presudu u ovoj formi 🙂

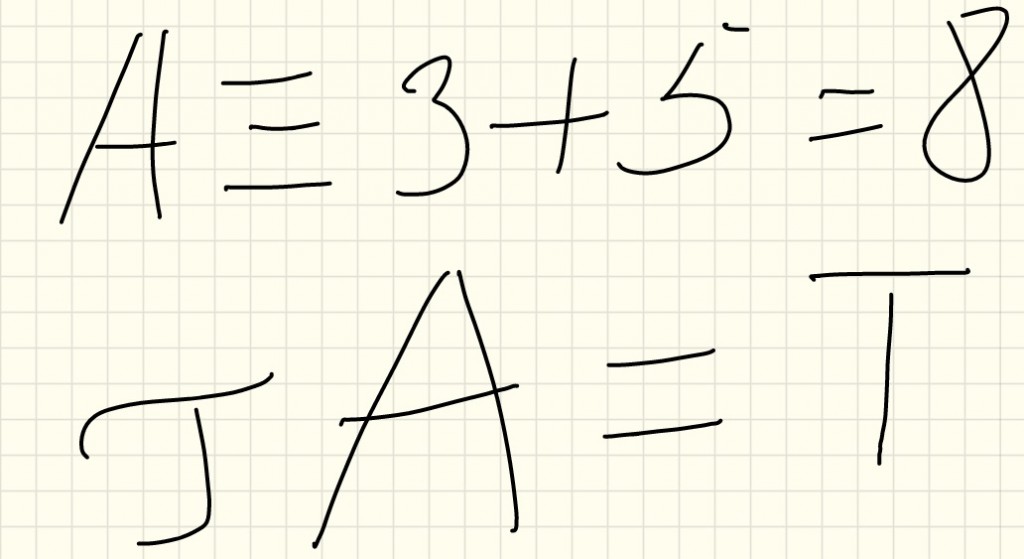























Poslednji komentari